作者:张凯，左袁德，赵捍军，马小鹏

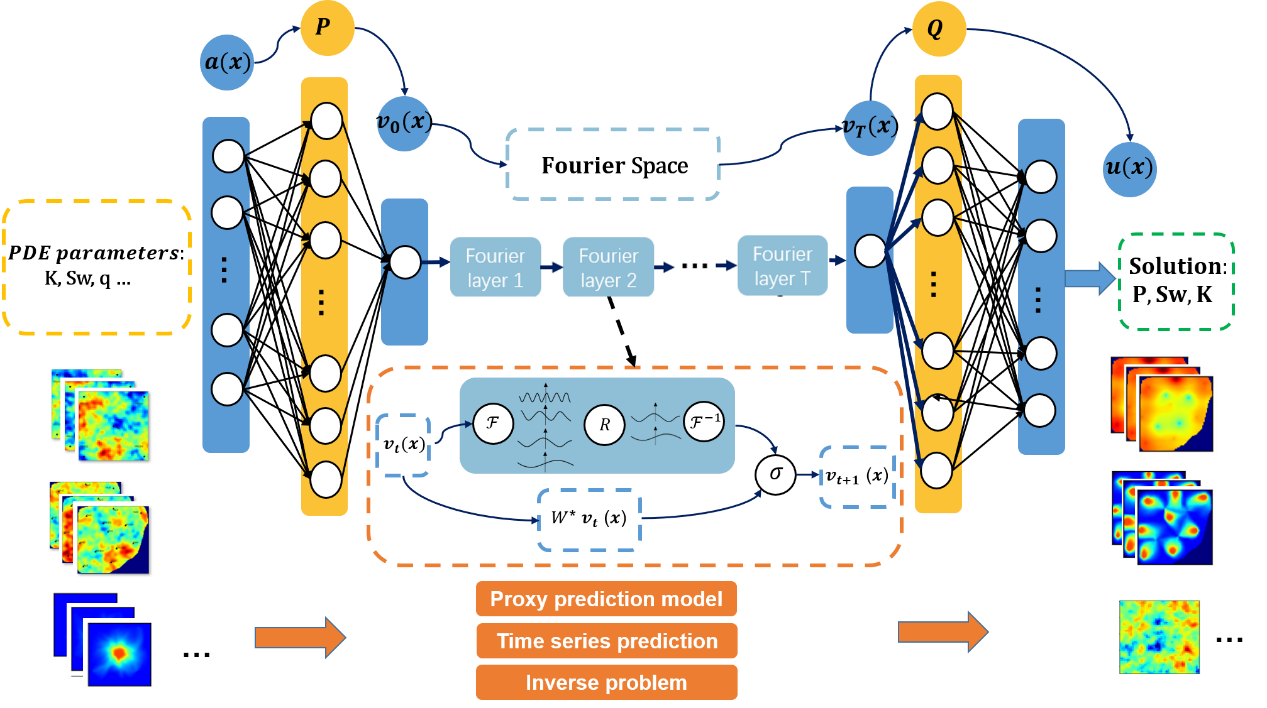
虽然深度学习在解决准确描述工程系统的偏微分方程（PDEs）方面取得了巨大的成功，但要获得复杂问题的高效、准确的解决方案，而不是传统的数值模拟，仍然是一个巨大的挑战。在储层工程领域，目前主流的机器学习方法已经成功应用。然而，这些流行的方法不能直接很好地解决二维两相油/水PDEs问题，而这是储层数值模拟的核心。傅里叶神经算子（FNO）是最近提出的一种高效的PDE求解结构，它克服了上述流行方法的缺点，在我们的工作中可以很好地处理这种类型的PDE问题。本文开发了一个基于深度学习的模型来解决基于FNO的地下二维油/水两相流PDE控制的三类问题。它在正向和反向问题上都取得了良好的效果。该网络使用快速傅里叶变换（FFT）来提取傅里叶空间的PDE信息，以近似微分算子，使网络更快，具有更大的物理意义。该模型是独立于网格的，具有良好的泛化能力，这也显示了超分辨率。与原来的FNO相比，我们改进了网络结构，增加了处理边界条件（BC）的物理约束，并使用形状矩阵来控制不规则边界。此外，我们还改进了FFT模块，使转换更加平滑。与先进的基于深度学习的不同分辨率的求解器相比，结果表明，该模型克服了流行算法的一些缺点，如物理信息神经网络（PINN）和完全卷积网络（FCN），具有更强的准确性和适用性。我们的工作在用神经网络替代传统数值方法进行储层数值模拟方面具有很大潜力

。

文章链接：https://doi.org/10.2118/209223-PA